중심화 경향이 뭘까?

통계 기초에 관해 공부하다 보면 central tendency (중심화 경향)라는 말이 나와요. 이게 뭘까요?

 

예를 들어서, 시험에서 80점을 맞았다고 해봐요. 잘 본걸까요 못 본걸까요? 그 시험을 본 사람들이 대체로 몇 점을 맞았는가에 따라서 기본적인 비교가 가능하겠죠? 중심화 경향은 어떠한 데이터를 대표하는 값을 구하는 거예요. 대표적으로는 산술평균, 중앙값, 최빈값이 있어요.

 

Mean (평균, 주로 산술평균 arithmetic mean)

가장 친근한게 이 평균값이죠? 평균값은 모든 수치를 더한 후 자료의 개수로 나눠줘요. 데이터가 {1, 2, 3} 이라면 평균값은 (1+2+3)/3 이게 평균값이예요. 

 

이 평균값은 균형점이라고 생각하면 좋아요. 

이렇게 균형을 잡고 있는데 데이터 하나가 추가되면서 16에 하나가 증가했다고 생각해봐요. 그럼 균형이 오른쪽으로 기울겠죠? 다시 평평하게 균형을 맞추기 위해서는 균형점이 오른쪽으로 옮겨가야 해요. 직관적으로 생각해보세요. 꽤 많이 가야겠죠? 

 

Median (중앙값)

여기서 중앙값을 생각해봐요. 중앙값은 말 그대로 중앙에 있는 값이예요. {1, 2, 3}의 중앙값은 2예요. {1, 2, 3, 4}의 중앙값은 2.5예요. 수식을 사용한다면 (2+3)/2 이게 중앙값이예요. 데이터의 수가 짝수인 경우에는 중앙에 두 값이 있으니 이 두 값의 평균이 중앙값이 되는거예요.

 

그럼 중앙값이 2.5일 때, 추가된 데이터가 16이라고 해봐요. 그럼 우리는 {1, 2, 3, 4, 16}이라는 데이터를 갖고 있죠? 중앙값은 3이 되겠네요. 위의 평균값과 비교해보면 어떤가요? 같은 16이라는 수치가 추가되었는데, 평균값의 경우는 꽤 많이 움직여야 하지만 중앙값의 경우는 겨우 0.5가 움직였어요. 즉, 데이터에 이상치(outliers)가 있는 경우에 평균값은 이에 항상 영향을 많이 받고, 중앙값은 대체로 적은 영향을 받아요. 

 

여기서 조금 더 생각해보세요.

데이터를 쭉 나열했을 때, 왼쪽에 데이터가 주로 모여있고 오른쪽 저 끝에 데이터가 찔끔 찔끔 보여요. 이렇게요.

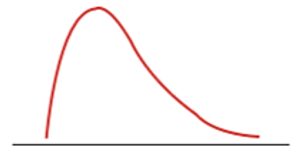
오른쪽 끝에 있는 수치들이 이상치들이죠? 그럼 평균값은 균형을 맞추기 위해 이 이상치들을 많이 쫓아가게 돼요. 하지만 중앙값은 이에 영향을 덜 받죠. 따라서 데이터가 위와 같이 오른쪽으로 꼬리가 달려 있다면, 평균값이 중앙값보다 더 오른쪽에 위치해요. 그럼 만약 왼쪽으로 꼬리가 달려 있다면요? 그럼 왼쪽으로 이상치가 더 많이 있다는 말이고, 평균값은 중앙값보다 더 왼쪽에 위치하겠죠? 

 

Mode (최빈값)

최빈값은 가장 빈도가 많은 포인트를 말해요. 위의 그래프에서 가장 위로 솓아있는 부분 있죠? 저 피크가 가장 빈도가 많은 포인트예요(y축이 빈도). 피크가 하나인 경우를 uni-modal 이라고 하고, 두 개면 bimodal, 혹은 그 이상이면 multimodal이라고 부르는데 뭐 이건 별로 중요하지 않고. 

 

이 최빈값은 언제 사용할 수 있을까요? 데이터의 척도가 명목척도 일 때 가장 쓸모가 있어요. 한국인이 좋아하는 음식들을 조사한 후 이를 대표하는 값을 도출하려고 해요. 1=김치찌개, 2=된장찌개, 3=치킨, 4=족발/보쌈, 5=자장면 등등이 있어요. 평균을 냈더니 3.5가 나왔어요. 의미가 전혀 없죠? 중앙값을 냈더니 3이 나왔어요. 이 역시 아무런 의미가 없어요. 이 중 오로지 최빈값만이 이를 가장 대표하는 값이예요. 

 

중앙값은 서열 척도를 사용했을 때 사용하기 좋아요. 일단 서열 척도의 경우에는 산술평균값은 의미가 없어요. 최빈값을 사용할 수 있지만 중앙값이 더 많은 정보를 줄 수 있어요. 그리고 비록 서열 척도가 아니더라도 이상치가 많거나 어느 한 쪽으로 많이 치우쳐진 데이터를 분석할 때 사용하면 좋아요.

 

마지막으로 평균값(산술평균값)은 데이터가 등간/비율 척도일 경우 그리고 이상치가 많지 않은 경우 사용하면 해당 데이터를 잘 대표하는 값을 얻을 수 있어요. 

 

만약 각 척도의 특징 구별이 잘 안된다면 가볍게 이 전 포스팅도 읽어보세요.

[통계 이야기/통계 기초(기술통계->추리통계)] - 척도 이제는 이해하고 넘어가자

 

 

이번 포스팅은 어떤 값이 데이터를 대표(중심)할 수 있는지에 대한, 즉 중심화 경향에 대해 알아봤어요. 다음 포스팅은 데이터 값들이 얼마나, 어떻게 퍼져있는지에 대해 생각해볼거예요. 

 

도움이 됐다면 커피 한 잔 사주시면 감사하겠습니다^^

EPIK is 어려운 지식을 가능한 한 쉽게 공유하는 곳이예요 :)