티스토리 뷰
[통계 이야기/PROCESS] - 조절효과 분석(Moderation) 결과 해석 이론
[통계 이야기/PROCESS] - PROCESS 조절효과(moderation) 분석 (GUI)
[통계 이야기/PROCESS] - PROCESS 다양한 조절(moderation)효과 분석 ◁ 현재 포스팅
저번 포스팅에서는 조절 변수가 하나인 단순한 조절 모형을 분석했어요.
만약 조절 변수가 2개 라면? (Model 2)
오늘은 조절 변수가 2개인 모형과 조절된 조절이라고 하나요? Moderated moderation을 분석해볼거예요.
때론 한 모형에 두 개의 조절변수를 넣고 싶을 수도 있어요. 매개분석의 경우에는 Model 4가 10개의 매개 변수를 처리할 수 있지만 조절 모형인 Model 1은 단 하나의 조절 변수만을 다룰 수 있어요. 조절 변수가 2개인 경우에는 model 2번을 사용해요.

이런 모델이예요.
분석은 간단해요. PROCESS를 열고,

종속변수는 Y variable에, 독립변수는 X variable에, 통제하고 싶은 변수가 있다면 Covariate(s)에,
조절변수1은 Moderator variable W에, 조절변수2는 Moderator variable Z에, 그리고 모델 넘버를 2로 바꿔주고요.
아래 처럼요.
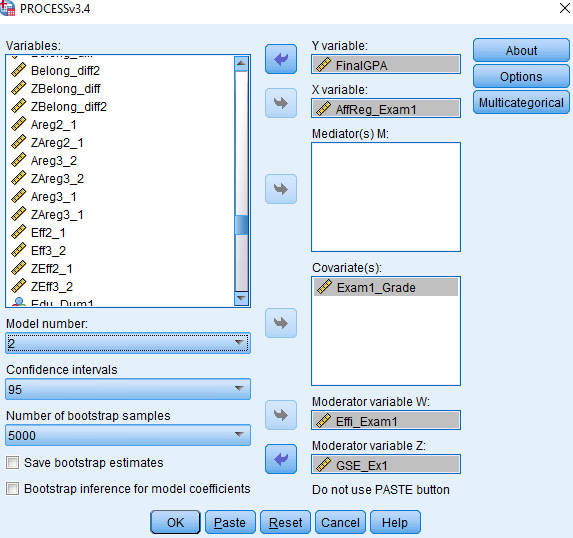
조절변수는 Effi_Exam1과 GSE_Ex1죠? 통제변수도 넣어줬어요.
Options 은 전 포스팅(위에 링크 있음) 참고해주세요.
결과를 보니,

흠... 조절변수1(Int_1)은 p=.0015로 유의한데, 조절변수2(Int_2)는 그렇지 않네요(p=.46)
이럴 경우는 어떻게 해야할까요? 이 상태로 해석을 해야할까요? 아님 조절변수2를 빼고 다시 분석을 해야할까요?
둘 다 괜찮아요. 아직 반드시 이렇게 해야한다는 합의점이 없어서 옳다고 생각하는데로 하시면 될 것 같아요.
조절 변수가 2갠데 moderated moderation? (Model 3)
이번에는 moderated moderation이예요. model 은 3번이예요.

이런 형태예요. 위와 똑같은데 모델 넘버만 3번으로 바꿔주면 돼요.
결과는 다음과 같아요.

모델 2번과 차이점이 뭐죠? 모델 3은 3-way 상호작용항이 있죠? Int_4가 3-way interaction term이예요.
가장 먼저 가장 높은 항을 봐요(top-down approach). 즉, Int_4가 유의한지 봐요. p=.27로 유의하지 않아요.
그럼 그 아래 항들(2-way interactions)을 봐요. ㅋㅋㅋ 어메 아무것도 유의하지 않네요.
그 다음은 각 main effects를 봐요. 이런 아무것도 유의하지 않아요.
우리의 목적을 위하여 ㅋㅋ 만약 이 상황에서 Int_1이 유의하다고 할게요.
그러면 Int_1을 probing하면 돼요. 이 부분은 전 포스팅과 같아요. 다시 말하면, AffReg이 FinalGPA에 주는 영향을
Effi_Exam1이 낮을 때, 평균일 때, 그리고 높을 때로 나누어서 비교하면 돼요.
만약 3-way interaction이 유의하다면?
그렇다면 만약 3-way 상호작용항(Int_4)이 유의하다면요? 이 의미는 moderated moderation 효과가 있다는 거고, X*W가 Y에 미치는 영향이 Z값의 변화에 따라 다르다는 의미예요. 그럼 대체 어떻게 다른걸까요?
좀 더 자세하게 살펴보기 위해 얘를 probing 해야 해요. 즉, AffReg*Effi_Exam1이 Final GPA에 주는 영향을 GSE_ex1이 낮을 때, 평균일 때, 그리고 높을 때로 나누어 비교하는 거예요. 이 전 포스팅과 이 포스팅을 잘 따라오셨으면 결과에 이런 값들도 있을거예요.
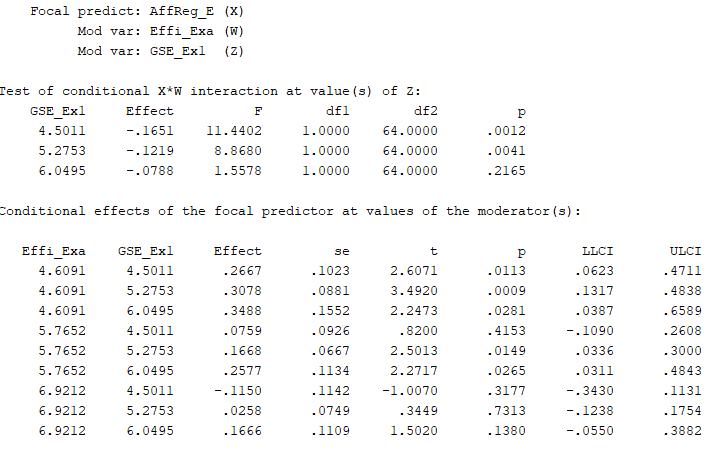
Test of conditional X*W interaction at value(s) of z
이게 제가 방금 말한거예요.
GSE가 낮을 때(=4.5011), AffReg*Effi_Exam1이 Final GPA에 주는 영향 = -.1651
.
.
어렵지 않죠? 이걸 Simple interactions이라고 해요. 이 simple interactions에서 GSE가 낮을 때와 평균일 때 AffReg*Effi_Exam1가 유의미하게 FinalGPA에 영향을 줘요(ps=각각 .0012 & .0041). 이 의미는 Z가 낮을 때와 평균일 때, X가 Y에 미치는 영향이 W값의 변화에 따라 다르다는 거예요. Z가 높을 때는 X가 Y에 미치는 영향이 W값의 변화에 따라 다르지 않다는 뜻이고요.
이젠 Z값이 낮을 때와 평균일 때, 각각 X가 Y에 미치는 영향이 W값의 변화에 따라 어떻게 바뀌는지 probing 해줘야해요. 즉, GSE(Z)를 고정해줬을 때(평균 혹은 -1SD), AffReg(X)이 FinalGPA(Y)에 주는 영향을 Effi_Exam1(W)이 낮을 때, 평균일 때, 높을 때로 나누어 비교해요. 위의 결과 창에서 conditional effects가 이거예요.
조절변수1(W)이 낮고 조절변수2(Z)가 낮을 때, X가 Y에 미치는 영향
조절변수1(W)이 낮고 조절변수2(Z)가 평균일 때, X가 Y에 미치는 영향
이런식으로 쭉 보여주는 거예요.
GSE가 낮을 때(=4.5011),
AffReg이 FinalGPA에 주는 영향이 Effi_Exam1이 낮으면(=4.6091) b=.2667이고 p=.0113로 유의하고,
Effi_Exam1이 평균이면(=5.7652) b=.0759이고 p=.4153으로 유의하지 않고,
Effi_Exam1이 높으면(=6.9212) b=-.1150이고 p=.3177로 유의하지 않네요.
이걸 simple simple slopes라고 해요.
이렇게 차례대로 분석을 하고 해석을 하시면 돼요.
이 외에도 다른 복잡한 경우들이 있어요.
예를 들어, 조절 변수가 categorical 변수들인데 그룹이 3개 이상이라거나, 결측치 때문에 multiple imputation을 했다거나, 상호작용항은 유의미한테 probing해보니 하나도 유의한게 없다거나, 아주 다양한 상황이 나올 수 있어요.
다 다루기가 힘드니 혹시나 이런 상황에 처하게 되면 댓글 남겨주세요.
즐거운 연구하세요!
도움이 됐다면 커피 한 잔 사주시면 감사하겠습니다^^
EPIK is 어려운 지식을 가능한 한 쉽게 공유하는 곳이예요 :)
Hey 👋 I just created a page here. You can now buy me a coffee!
www.buymeacoffee.com
'통계 이야기 > PROCESS' 카테고리의 다른 글
| PROCESS 설치 [업데이트] (4) | 2024.07.01 |
|---|---|
| PROCESS 매개+조절 모형 분석 (4) | 2020.05.16 |
| PROCESS 조절효과(moderation) 분석 (GUI) (8) | 2020.05.14 |
| 조절효과 분석(Moderation) 결과 해석 이론 (4) | 2020.05.13 |
| PROCESS 간접효과 분석 (syntax 심화) (0) | 2020.05.12 |
- invariance test
- SEM
- 매개효과
- 소속감
- 구조방정식
- 조절분석
- EFA
- Mplus
- rstudio
- probing
- 프로세스
- structural equation modeling
- 논문통계
- moderation
- exploratory factor analysis
- 간접효과
- close relationships
- process
- social exclusion
- mediation
- R 기초
- 탐색적 요인분석
- Hayes
- amos
- indirect effect
- 부정적 평가 두려움 척도
- MLM
- process macro
- multilevel
- 사회심리
