티스토리 뷰
SEM 분석에는 많은 과정이 있어요.
Theorization
Specification
Identification
Estimation
Evaluation
Modification or Respecification
Theorization은 말 그래도 theory를 세우는 거예요. 우리가 무턱대고 모델을 만드는게 아니잖아요? 다 이론에 근거해 모델을 만들잖아요. 이론을 통해 난 어떤 연구를 할꺼야 라고 정했어요.
Specification은 이러한 theorization을 통해 모델을 만드는 거예요. 모델을 만들기 위해서는 이론을 제외하고도 다른 지식들이 필요해요. 오늘은 이 Specification을 하는 과정에서 필요한 것들에 대해 알아볼게요.
RAM notation 규칙
바로 전 포스팅에서 RAM notation 이 어떤건지 설명했어요. 먼저 이 RAM notation의 규칙을 알면 미래가 편해요.
아 그 전에 exogenous 와 endogenous 변수의 차이를 아시나요?
Endogenous 변수는 "from within"이라는 뜻이예요. 한국어로는 내생변수라고 하나요?
즉, 우리가 만드는 모델 "안에 있는 어떤 변수"한테 영향을 받는 변수를 뜻해요.
따라서 다른 변수한테 화살표를 "받는" 변수는 endogenous 변수예요.
Exogenous 변수는 "from outside"라는 뜻이예요. 외생변수?
즉, 우리가 만드는 모델 "밖에 있는 어떤 변수"한테 영향을 받는 변수예요.
따라서 모델 안에서는 아무한테도 화살표를 받지 않아요.
A -> B -> C
A는 exogenous variable
B와 C는 endogenous variables
어렵지 않죠?
이번엔 RAM notation 복습.
ㅁ : 네모는 관찰된 변수
<-> (sling) : 양방향 화살표는 상관관계
-> : 일방향 화살표는 경로계수
ㅇ : 원은 잠재변수 혹은 오차

자 이제 드디어 RAM notation의 규칙.
아래 모델을 예시로 들어볼게요.

모든 exogenous 변수들은 반드시 분산이 붙어있어야 해요. A -> C 라면 A가 exogenous 변수죠?
따라서 A에는 위의 분산이 반드시 있어야 해요. B에도 똑같이 분산이 붙어있어야 겠죠? A와 B 위에 양방향 화살표가 보이죠? 이게 분산이 붙어있는 거예요. 그럼 C는 어떨까요?
모든 endogenous 변수들은 반드시 오차항이 있어야 해요. A -> C 라면 C가 endogenous 변수이고,
C <- e 이렇게 오차가 붙어야 해요. Endogenous 변수들은 분산이 붙지 않아요. 즉, C에는 분산이 있으면 안돼요. 하지만 e에 분산이 붙어있는건 보이죠? e역시 아무에게도 화살표를 받지 않아요. 따라서 분산이 붙어요. 원리는 어려울지 몰라도 규칙은 쉬워요. 화살표를 안받으면 분산을 붙여라.
Sling (양방향 화살표)은 exogenous 와 exogenous 변수끼리만 연결해줘요. A와 B가 연결된거 보이죠?
A -> B -> C 이런 모델에서는 sling을 그려서는 안돼요. Exogenous 변수가 하나밖에 없잖아요.
자유도
논문을 보면 가끔 이 저자가 독자들 모르게 선 하나를 더 긋지 않았을까? modification indices를 통해 적합도를 올렸지만 그 사실을 논문에는 적지 않은거 아닐까? 이런 생각 해본 적 없나요? 그럴 때는 자유도를 계산해보면 돼요.
자유도 = Total elements - Free parameters 로 계산해요. 겁먹지 마요. 쉬워요.
Total elements = (V*(V+1))/2
여기서 V는 관찰된 변수(네모)의 수 예요. 관찰된 변수가 5개라면, (5*6)/2 = 15
쉽죠잉? 곧 그림으로도 볼게요.
그럼 free parameters는 뭔가?! 이 말의 뜻은 "앞으로 추정될 놈들"이예요.
예를 들어, A -> B 라고 하면, 우리가 아직은 -> 이 경로의 값은 모르지만 나중에 데이터를 집어넣어서 값을 얻을거잖아요? 이렇게 앞으로 추정될 놈들이 free parameters예요.
위의 모델을 다시 한 번 봐볼게요.

자 이 모형의 자유도는 얼마일까요?
먼저 관찰된 변수의 수는 3개죠?
그럼 total elements = (3*4)/2 = 6
Free parameters 는 몇개일까요?

6개죠? 따라서 이 모형의 자유도 = 0 이예요.
다른 모형을 볼까요?
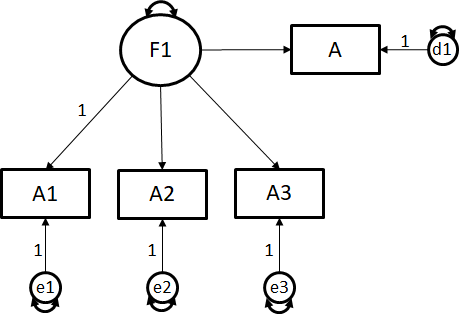
관찰된 변수의 개수는 몇 개인가요? 네모가 관찰된 변수죠? 따라서 4개.
그럼 total elements = (4*5)/2 = 10
Free parameters 는요?

8개죠? 따라서 자유도 = 10-8 = 2
다음 모형의 자유도를 한 번 계산해보세요.

답만 가르쳐 드릴게요. 답은 12입니다!
자유도가 어떻게 계산되는지 아는건 SEM의 기초중의 기초겠죠? 하다보면 재밌어요 ㅋㅋㅋ 열논문 하세요^^
도움이 됐다면 커피 한 잔 사주시면 감사하겠습니다^^
EPIK is 어려운 지식을 가능한 한 쉽게 공유하는 곳이예요 :)
Hey 👋 I just created a page here. You can now buy me a coffee!
www.buymeacoffee.com
'통계 이야기 > SEM 기초 및 Amos' 카테고리의 다른 글
| SEM 적합도 올리기 (0) | 2020.05.18 |
|---|---|
| 구조방정식 적합도 (0) | 2020.05.18 |
| 구조방정식(SEM) 이론 기초 4 (0) | 2020.05.18 |
| 구조방정식(SEM) 이론 기초 3 (2) | 2020.05.18 |
| 구조방정식(SEM) 이론 기초 1 (0) | 2020.05.17 |
- 조절분석
- process macro
- 탐색적 요인분석
- EFA
- R 기초
- close relationships
- 간접효과
- SEM
- social exclusion
- invariance test
- 구조방정식
- moderation
- probing
- MLM
- Hayes
- 매개효과
- exploratory factor analysis
- structural equation modeling
- amos
- Mplus
- mediation
- process
- 프로세스
- 부정적 평가 두려움 척도
- indirect effect
- 사회심리
- 소속감
- multilevel
- rstudio
- 논문통계
