티스토리 뷰
자 오늘부터 프로세스 모델 넘버순으로 차근차근 살펴보려고 해요.
버전별로 모델 넘버가 달라질 수 있으니 참고하시고, 제가 사용하는 버전은 4.2입니다.
오늘 다룰 모델 1번은 아래 그림과 같아요.
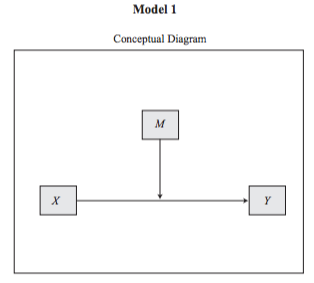
하나의 조절변수가 X → Y에 영향을 미치는지 볼 때 사용하는 모델이네요.
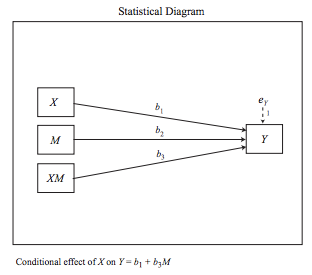
우리가 조절변수의 영향을 볼 때 어떻게 계산하죠? Interaction term, 즉 상호작용항을 만들어서 회귀식에 넣죠?
즉, X가 독립변수, Y가 종속변수, M이 조절변수일 때,
Y = a + b1X + b2M + b3XM
위의 회귀식을 통해서 우리는 조절변수의 영향이 있는지 알아볼 수 있어요.
PROCESS도 이와 같은 회귀식을 이용해서 분석을 해요.
SPSS 데이터 파일 열어놓으셨죠?
PROCESS 설치는 하셨나요?
안하셨다면 아래 포스팅 보시고 설치 먼저 하시고요.
PROCESS 설치 [업데이트]
[통계 이야기/PROCESS] - PROCESS 설치 [구버전] PROCESS 설치PROCESS는 쉽게 말하면 복잡한 매개 분석이나 조절 분석 등을 쉽게 해주는 툴이라고 생각하면 돼요. 상당히 유용하면서, 신뢰도 높고, 다소 정
study-easy.tistory.com
PROCESS 세팅
분석(Analyze) → 회귀분석(Regression) → PROCESS로 가시면 다음과 같은 창이 떠요.

오늘 사용할 변수는 DP(종속변수), MOD(조절변수), IND(독립변수)예요.
각각의 변수를 알맞게 넣어볼게요.
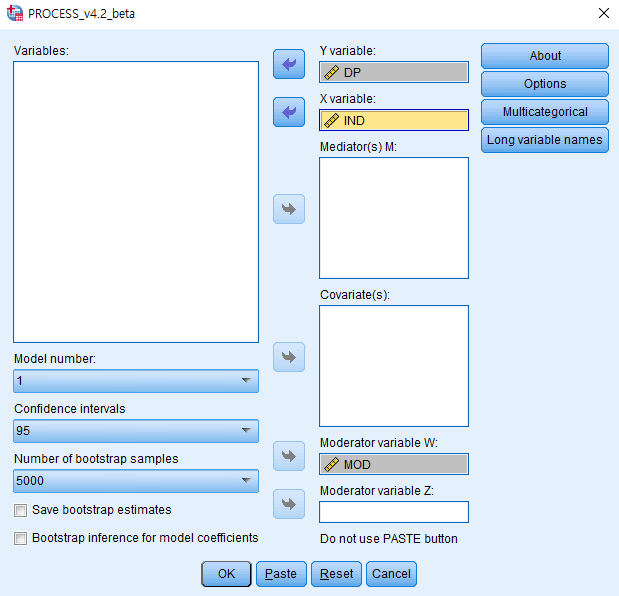
PROCESS에서는 조절변수가 W로 표현이 되니 참고하세요.
만약에 통제변수가 있다면 Covariate(s)에 넣어주시면 돼요.
왼쪽부터 차근차근,
오늘 사용할 Model number는 1번이예요.
위에서 말한것처럼 1번은 조절변수가 1개인 모델이예요.
Confidence intervals, 즉 신뢰구간은 95로 해주세요.
p값 비슷한거라고 생각하시면 돼요.
Numver of bootstrap samples는 특별한 이유가 있지 않으면 5,000개로 하시면 돼요.
Bootstrapping이란건 내가 갖고 있는 데이터에서 표본을 추출하는 거예요. 즉, 5,000개의 뜻은 내 데이터에서 5,000개의 표본을 추출한다는 의미예요.
결론적으로는 왼쪽에서는 model number만 원하는 숫자를 골라주시면 돼요.
오른쪽으로 가면 Options, Multicategorical, 그리고 Long variable names 이 세가지 메뉴가 있죠?
먼저 Options을 볼게요.

뭐가 많죠?
저걸 다 설명하기 보다는 일단 오늘 필요한 것들만 설명해볼게요.
Generate code for visualizing interactions
말 그대로 interaction을 시각화할 수 있는 코드를 생성해주는 거예요.
이 부분은 나중에 결과창을 보면서 더 얘기해볼게요.
Decimal places in output
소수점 몇째자리까지 볼지 선택하시면 돼요.
Mean center for construction of products
centering에 관한거예요. Centering은 각 변수에서 평균값을 빼주는거예요. 각각의 관측된 값이 평균에서 얼마나 떨어져있는지를 나타내줘요. 이 부분에 대한 자세한 내용은 검색하시면 충분히 나올거예요.
All variables that define products 는 필요한 변수 모두 centering 시켜줘요. 현재 모델에서는 독립변수와 조절변수.
Only continuous variables that define products 는 범주형(categorical)변수는 제외하고 centering 해줘요. 만약 변수들이 모두 연속형이라면 어떤걸 선택해도 같은 결과가 나와요.
Probe interactions
나중에 상호작용항이 유의미하게 나오면 probing이란걸 하게되요. 여기서는 언제 이 probing을 하겠냐 를 물어보고 있어요.
Conditioning values
이건 조절변수가 어떤 값일때 X → Y 를 보여줄까를 물어보는 거예요.
예를 들어, -1SD, Mean, +1SD를 선택하면 조절변수가 -1SD일때 X → Y, 평균일때 X → Y, +1SD일때 X → Y를 각각 보여줘요.
Johnson-Neyman output
이건 조절 변수가 특정 값일 때 독립 변수의 효과가 유의하게 달라지는 지점을 확인하는 데 사용할 수 있어요. 나중에 결과값 보면 이해되실거예요.
자, 저의 세팅은 다음과 같아요.

조절효과를 분석할 때 centering은 필수라고 생각하는 분들이 계신데 그렇지 않아요. 하면 괜히 결과 해석만 헷갈려져요.
필요하면 하고, 딱히 이유가 없으면 하실 필요 없어요.
Continue 눌러주시고,
그 다음에는 Multicategorical이 있어요.
누르면 다음과 같은 창이 떠요.

만약 변수 중에 범주형(categorical) 변수가 있다면 여기서 설정해줘야해요.
오늘 보여드릴 예시는 전부 연속형이라 이 부분은 세팅할 필요는 없어요.
근데 만약 갖고 계신 데이터에서 조절변수가 범주형이라면, Variable W에서 Multicategorical에 체크를 해주시고 Coding system에서 알맞은 종류 선택하시면 돼요.
Multicategorial 아래에는 Long variable names가 있어요.

만약 변수 이름이 길다면 I accept the risk of incorrect output. 이 부분에 체크를 하셔야 돼요.
PROCESS에서는 변수 이름의 8글자를 사용하나봐요.
만약 두 변수의 이름이 비슷해서 앞 8글자가 같다면 부정확한 결과가 나올 수 있는 것 같아요.
따라서 만약 변수명이 길다면 저기에 체크해주시고, 긴 변수 이름들이 비슷하다면 바꿔주세요.
저는 다 짧으니 체크할 필요가 없겠죠?
자 이대로 돌려줄게요.
결과 분석
자 결과를 차근차근 볼까요?
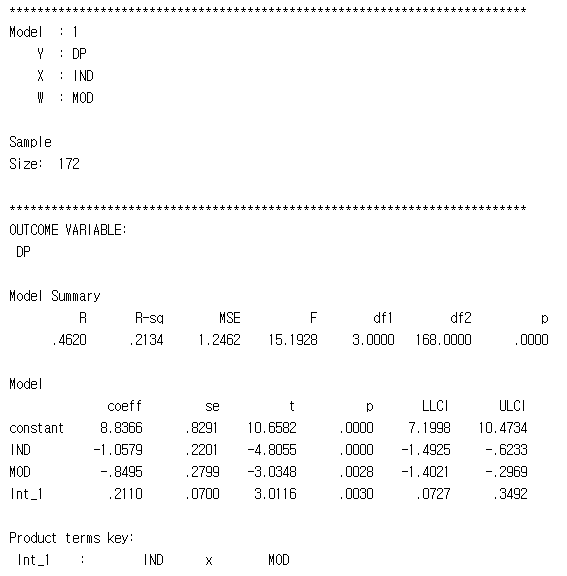
Model 1번으로 돌렸고, 종속변수는 DP, 독립변수는 IND, W로 표시되는 조절변수는 MOD네요.
전체 샘플 사이즈는 172개고요.
그 아래는 조절효과 분석을 위한 다음과 같은 회귀식 분석 결과예요.
Y = a + b1*IND + b2*MOD + b3*Int_1
여기서 중요한 건 Int_1의 결과죠?
조절 변수의 영향 여부는 상호작용항(interaction term)이 유의한지에 달려있어요.
Int_1은 IND x MOD, 즉 상호작용항이고, 이 부분의 p값은 .003이예요.
그리고 옆에 LLCI 그리고 ULCI는 95% 신뢰구간에서 0을 포함하고 있지 않아요. Lower level (.25) 에서는 .0727 그리고 upper level (.975)에서는 .3492 이라는 의민데 다 빼고, 저 두 값 사이에 0을 포함하지 않으면 (95% 신뢰구간에서) 유의하다 라고 말할 수 있어요.
따라서 결론적으로는 조절효과가 있다는거죠.
조절효과가 있으면 사실상 독립변수인 IND의 영향이나 조절변수인 MOD의 영향은 의미가 없어요.
조절효과가 있으면 무조건 simple slope분석을 해야해요.
만약에 상호작용항이 유의하지 않다면 main effects, 즉 IND와 MOD의 영향을 해석하시면 돼요.
여기서는 상호작용항이 유의하기 때문에 simple slope (=simple effect, conditional effects, etc.) 분석으로 넘어갈거예요.
Probing
아래 결과를 보시면 conditional effects라고 하고 있어요.
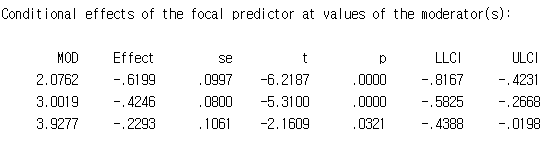
이게 simple effects (slopes)예요.
Options에서 -1SD mean +1SD로 설정을 바꿨기 때문에, 조절효과의 낮은 값(2.0762)은 저 변수의 -1SD 값이고 높은 값(3.9277)은 +1SD 값이예요. 중간값(3.0019)은 평균값이고요.
보시면 MOD 값이 낮을 때(2.0762) p값(=.0000)이 유의한거 보이죠? 즉, MOD가 낮을 때, IND가 DP에 영향을 미친다고 할 수 있어요. Effect가 음수이기 때문에 음의 방향으로, 즉 부정적인 영향을 준다고 말하면 되겠네요.
MOD의 평균 값이나 높은 값 역시 p값이 .05 수준에서 유의해요.
근데 조절효과가 있다는 의미는 뭔가요? MOD가 변화함에 따라서 IND가 DP에 주는 영향이 바뀐다는 거잖아요?
여기서 나타난 결과는 MOD가 변화함에 따라서 IND가 DP에 주는 영향의 크기가 유의하게 바뀌고 있다는 거예요. 즉, MOD가 높아질수록 IND가 DP에 미치는 영향이 약해지고 있죠. 반면에 만약 상호작용항(Int_1)이 유의하지 않았다면 MOD가 변화해도 IND가 DP에 미치는 영향이 달라지지 않는다고 해석해야겠죠.
그 다음에 나타나는 Johnson-Neyman (JN) output을 봐볼까요?
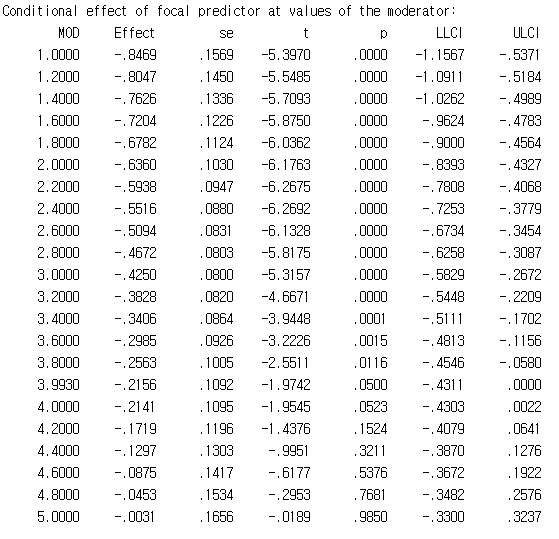
이건 독립변수랑 종속변수간의 관계 변화를 조절변수 관점에서 보여주는 거예요.
가장 왼쪽이 조절변수(MOD) 값이예요. 조절변수 값이 점차 커짐에 따라, p값이 유의하다가 점점 커지는거 보이시나요?
그러다가 MOD값이 3.9930 이후에는 p값이 .05 수준에서 유의하지 않아지게 돼요.
이 뜻은 MOD값이 1부터 3.9930 사이에서는 IND가 DP에 미치는 영향이 유의한데 그 이후에는 유의하지 않다는 의미예요. 이렇게 조절변수의 값에 따라서 독립변수가 종속변수에 미치는 영향의 유의성 영역을 보여줘요. 별로 어려운건 아니죠?
Visualization. 그래프 만들어 보기
Options 에서 visualization을 위한 code 만들기에 체크했었죠?
그럼 다음과 같은 결과값이 떠요.

이걸 모두 복사하시고 SPSS에서 syntax창을 열어주세요.

그럼 syntax창이 뜰거예요.
여기다가 다음과 같이 붙여넣기 해주세요.

자, 여기서 모두 선택한 다음 위에 보이는 Run Selection 버튼을 눌러주세요.
그럼 다음과 같은 그래프가 나올거예요.
*참고로 이 그래프는 참고용으로만 쓰세요. 논문에 들어갈 그래프는 위의 값을 이용해서 새롭게 만들어주세요. SPSS 결과 표나 그래프를 논문에 그대로 쓰면 안돼요.*
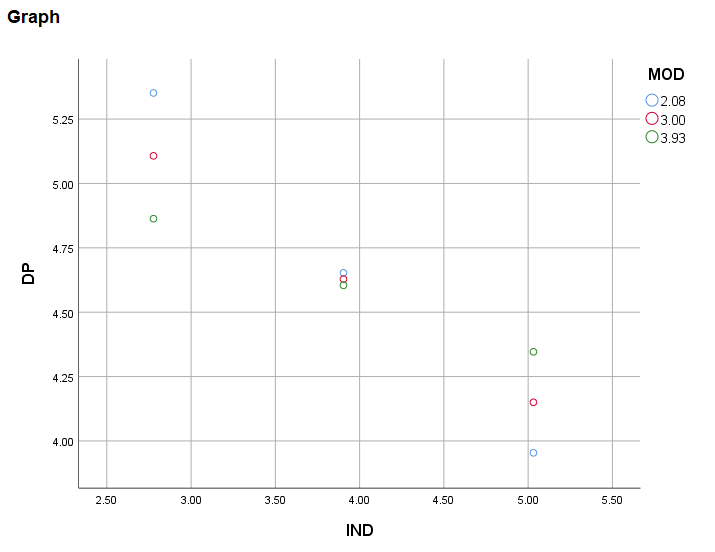
이게 개인적으로는 선 없이는 그래프가 헷갈리더라고요. 그래서 저는 주로 선을 그어줘요.
저 표를 더블클릭 하시고 아래 사진에 표시된 곳을 클릭하시면 자동으로 선이 추가돼요.
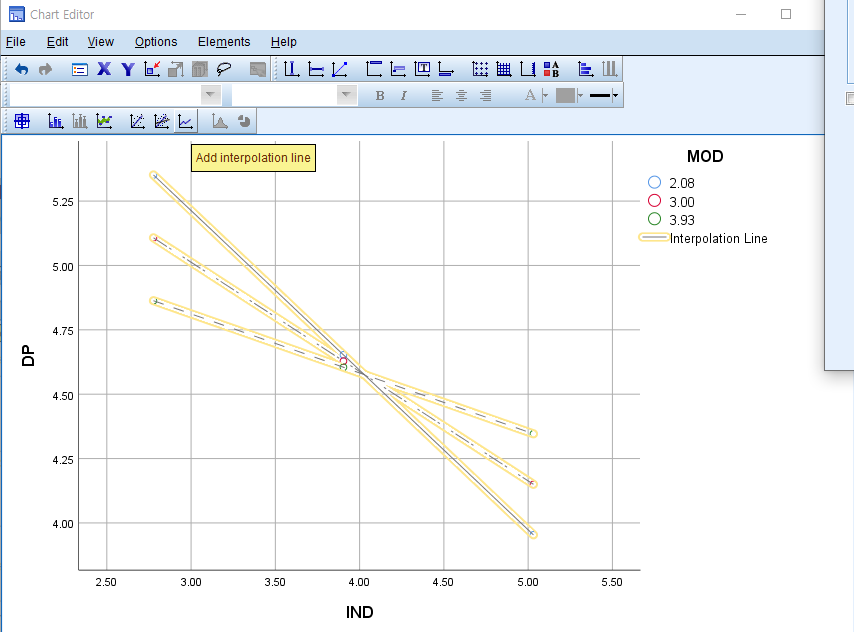
저 Add interpolation line을 누르면 팝업창이 하나 뜨는데 그냥 닫아주시면 돼요.

자, 이렇게 그래프로 보니 좀 더 명확하죠?
1. 상호작용항이 p값 .05 수준에서 유의했어요.
2. 그래서 simple effects를 봤더니 조절변수가 커질수록 IND가 DP에 미치는 영향이 약해졌어요.
3. 그래프를 보니 MOD가 낮을때(2.08, 파란색) 회귀선의 기울기가 MOD가 높을때(3.93, 초록색)보다 훨씬 가파르죠.
이렇게 하면 PROCESS model 1을 이용한 조절 효과 분석이 끝나요.
다음에는 model 2로 돌아올게요.
'통계 이야기 > PROCESS' 카테고리의 다른 글
| PROCESS 설치 [업데이트] (4) | 2024.07.01 |
|---|---|
| PROCESS 매개+조절 모형 분석 (4) | 2020.05.16 |
| PROCESS 다양한 조절(moderation)효과 분석 (4) | 2020.05.14 |
| PROCESS 조절효과(moderation) 분석 (GUI) (8) | 2020.05.14 |
| 조절효과 분석(Moderation) 결과 해석 이론 (4) | 2020.05.13 |
- MLM
- 사회심리
- indirect effect
- Hayes
- process
- 조절분석
- SEM
- 소속감
- 매개효과
- social exclusion
- close relationships
- invariance test
- structural equation modeling
- 구조방정식
- EFA
- process macro
- amos
- moderation
- R 기초
- 간접효과
- 탐색적 요인분석
- 논문통계
- probing
- exploratory factor analysis
- multilevel
- 프로세스
- Mplus
- mediation
- 부정적 평가 두려움 척도
- rstudio
